Problem Statement
Description
You are climbing a staircase. It takes
nsteps to reach the top.Each time you can either climb
1or2steps. In how many distinct ways can you climb to the top?
Examples
Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
Constraints:
1 <= n <= 45
Key Insights
First Principles Derivation
The problem asks us to count the number of ways a person can climb a set of n stairs taking 1 or 2 steps per move. Before we can solve this problem for n stairs, we will need to know the answer for the first few stairs. Once we understand the base cases, we can build out a general solution.
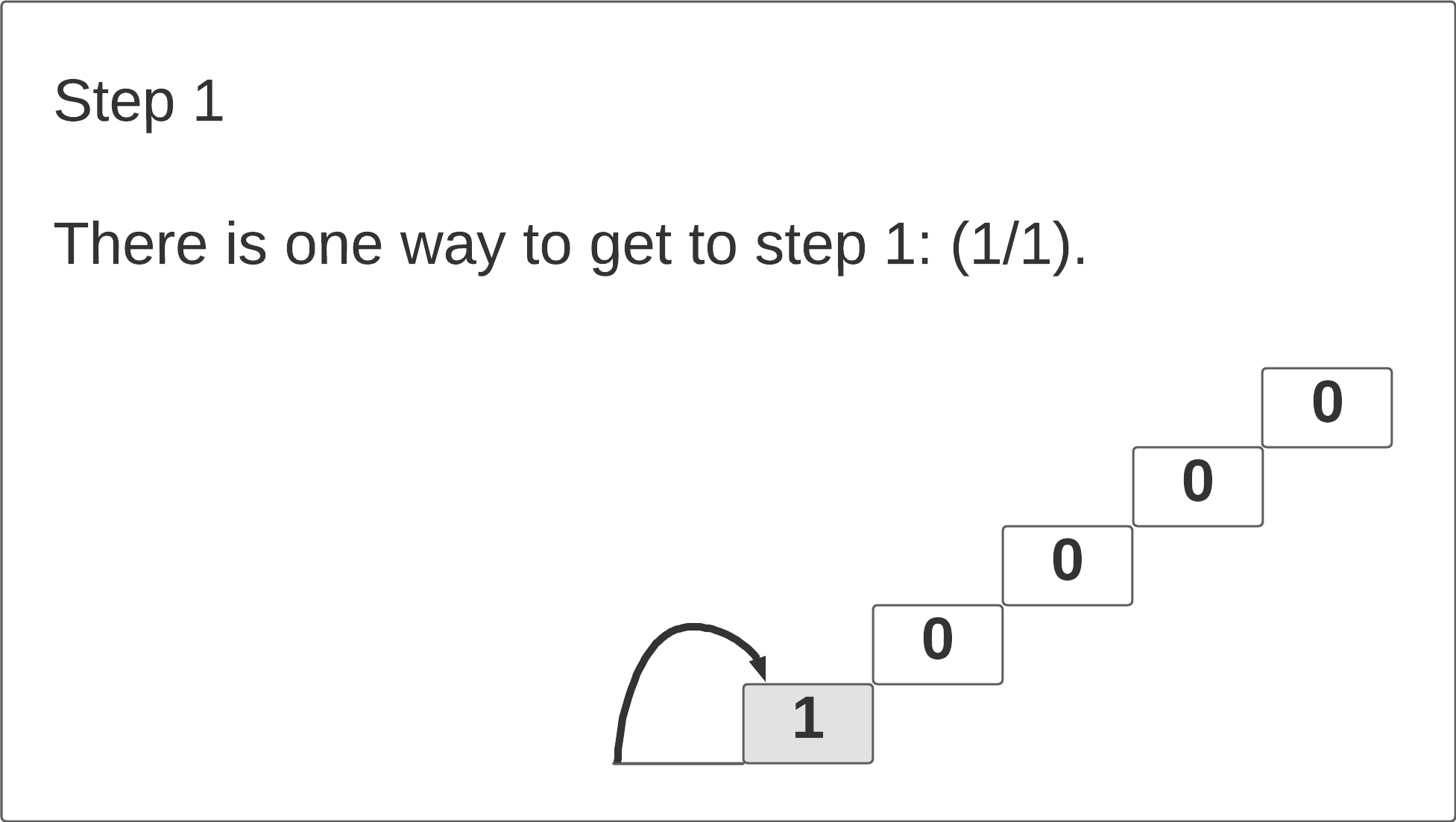
How many different ways can we climb to the 1st stair? There is only 1 way: we can only take 1 step.
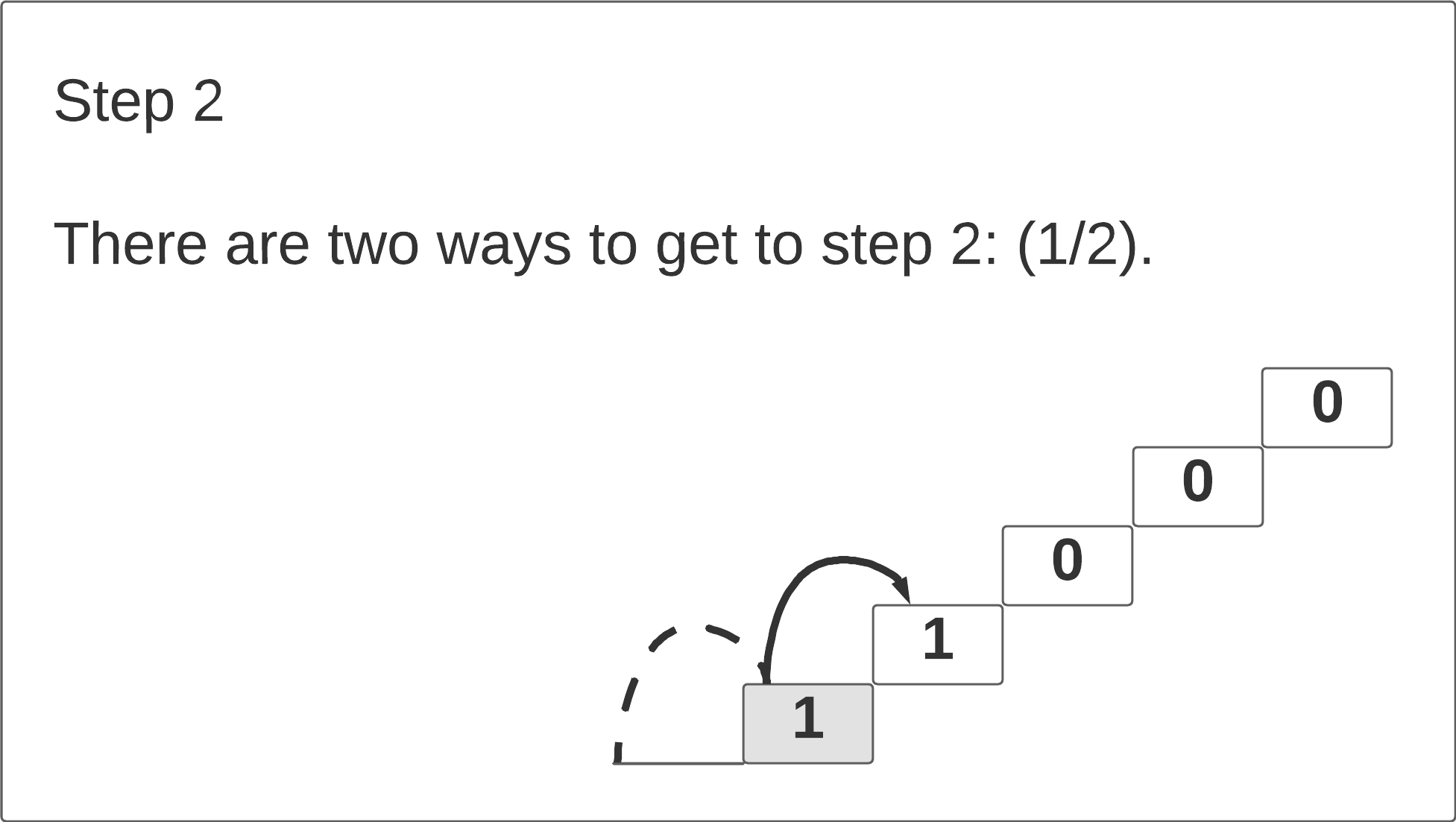
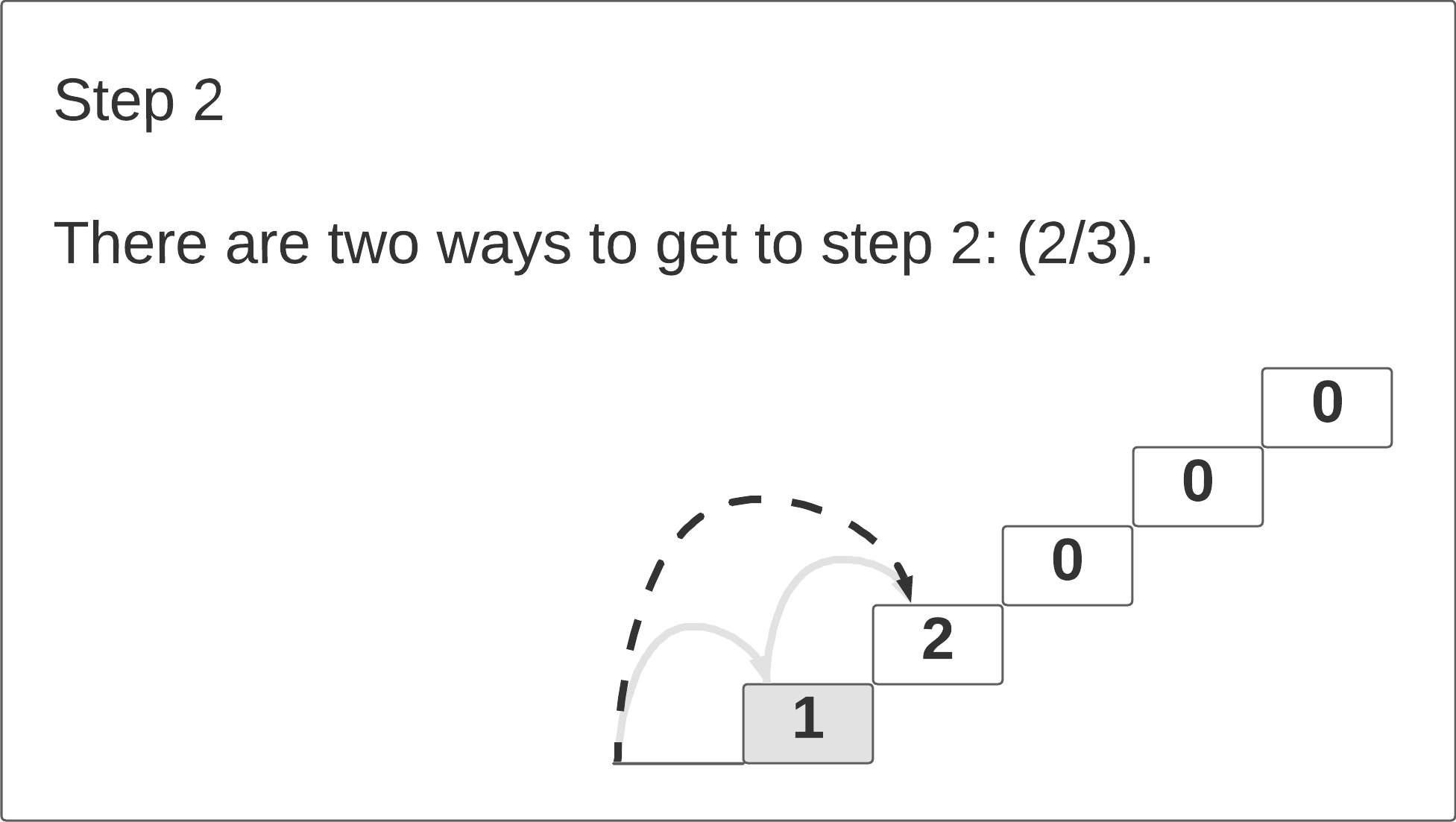
How many different ways we climb to the 2nd stair? There are 2 ways: we can take 2 single steps or we can take 1 double-step stride.
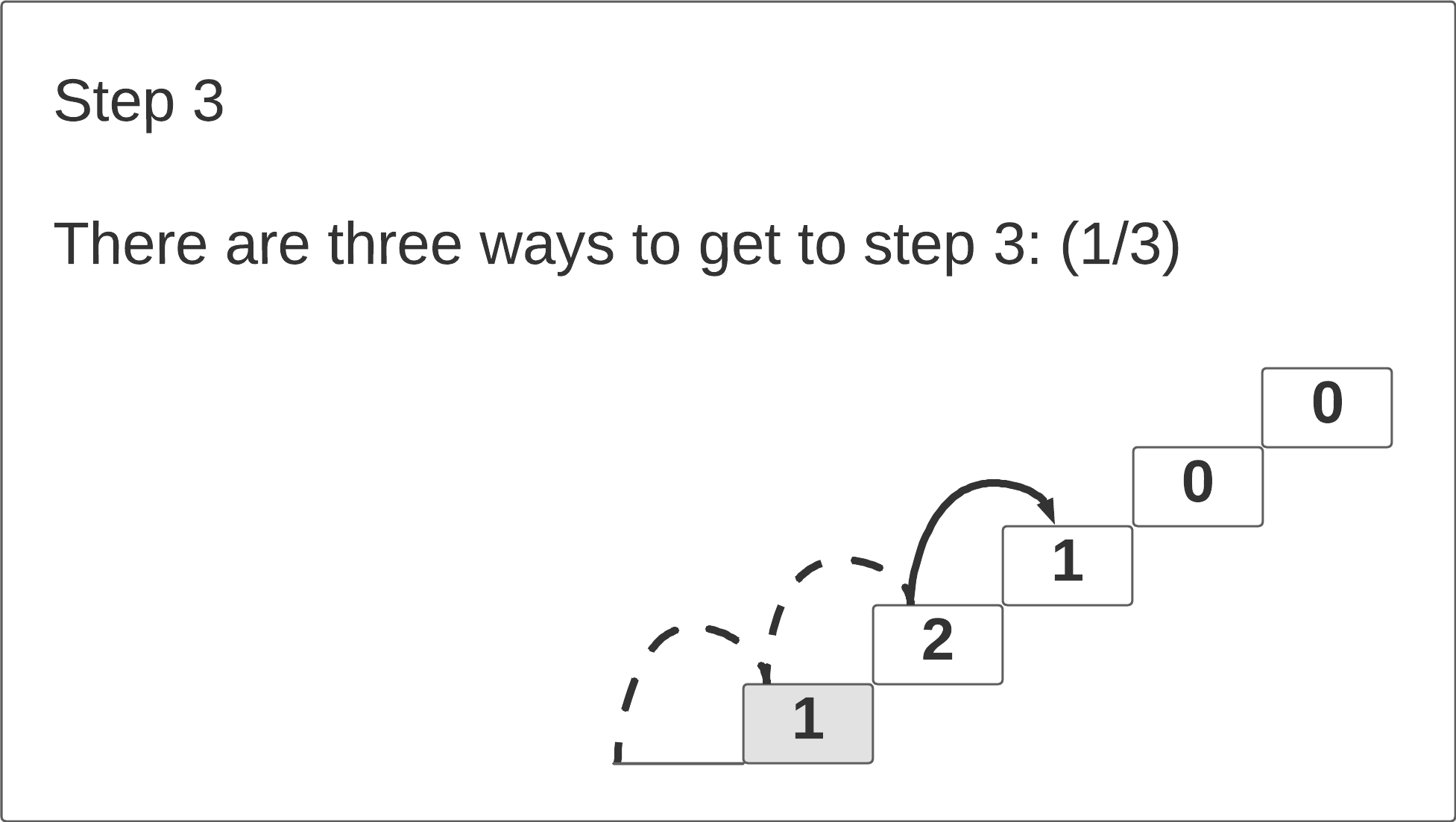
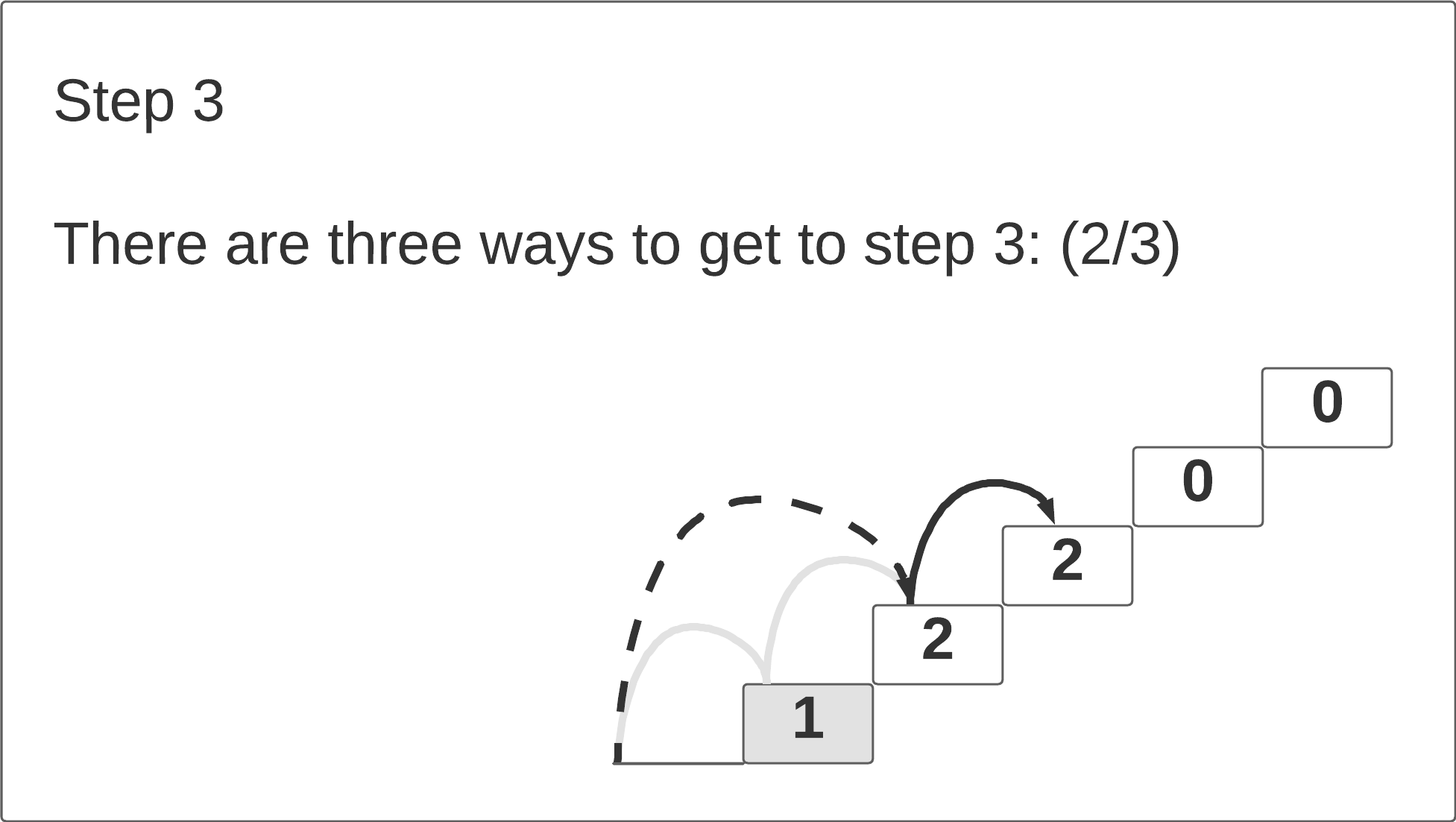
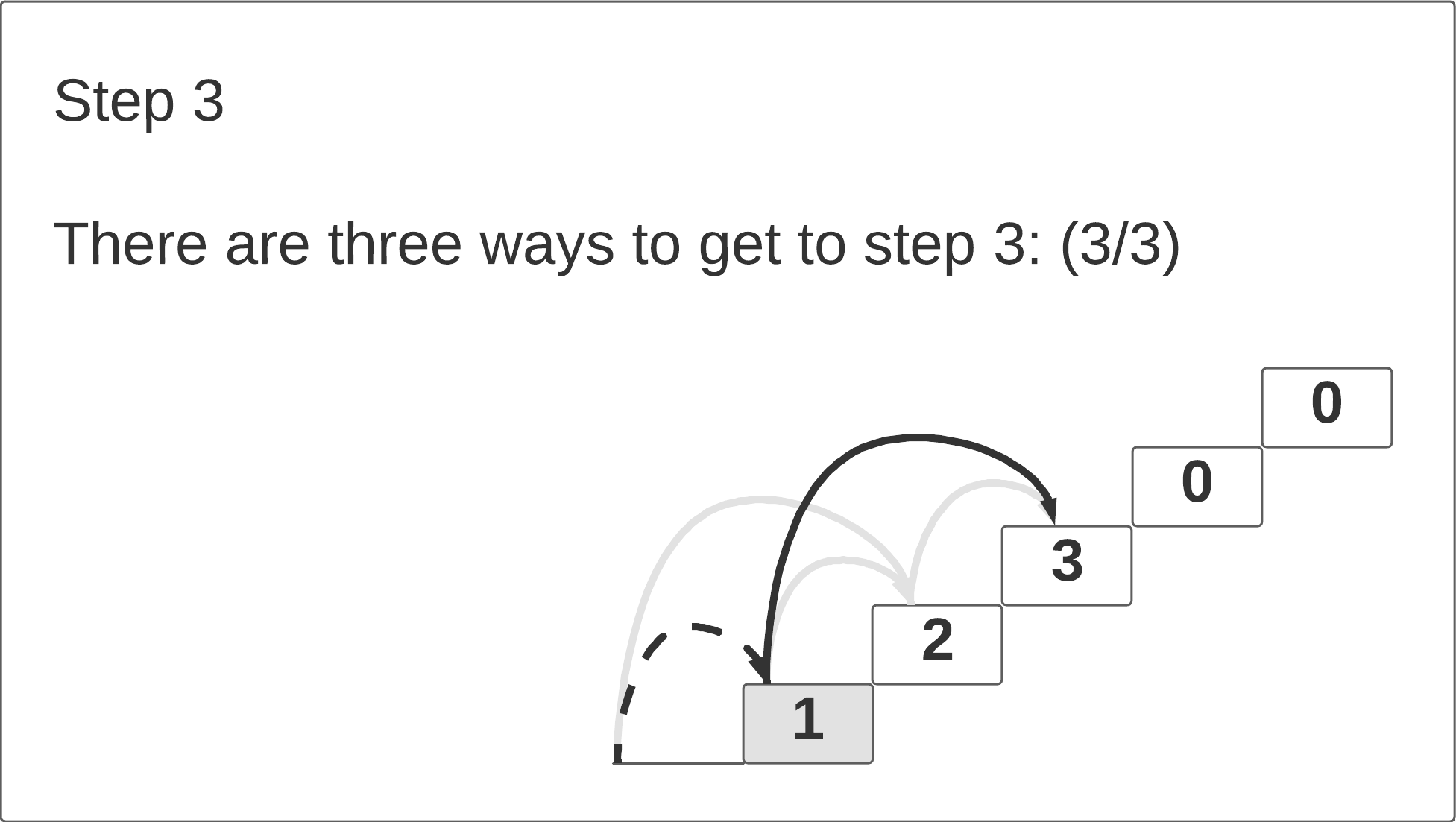
How many different ways can be climb to the 3rd stair? There are 3 ways: we can take 3 single steps; 1 double-step and 1 single-step; or 1 single-step and 1 double-step.
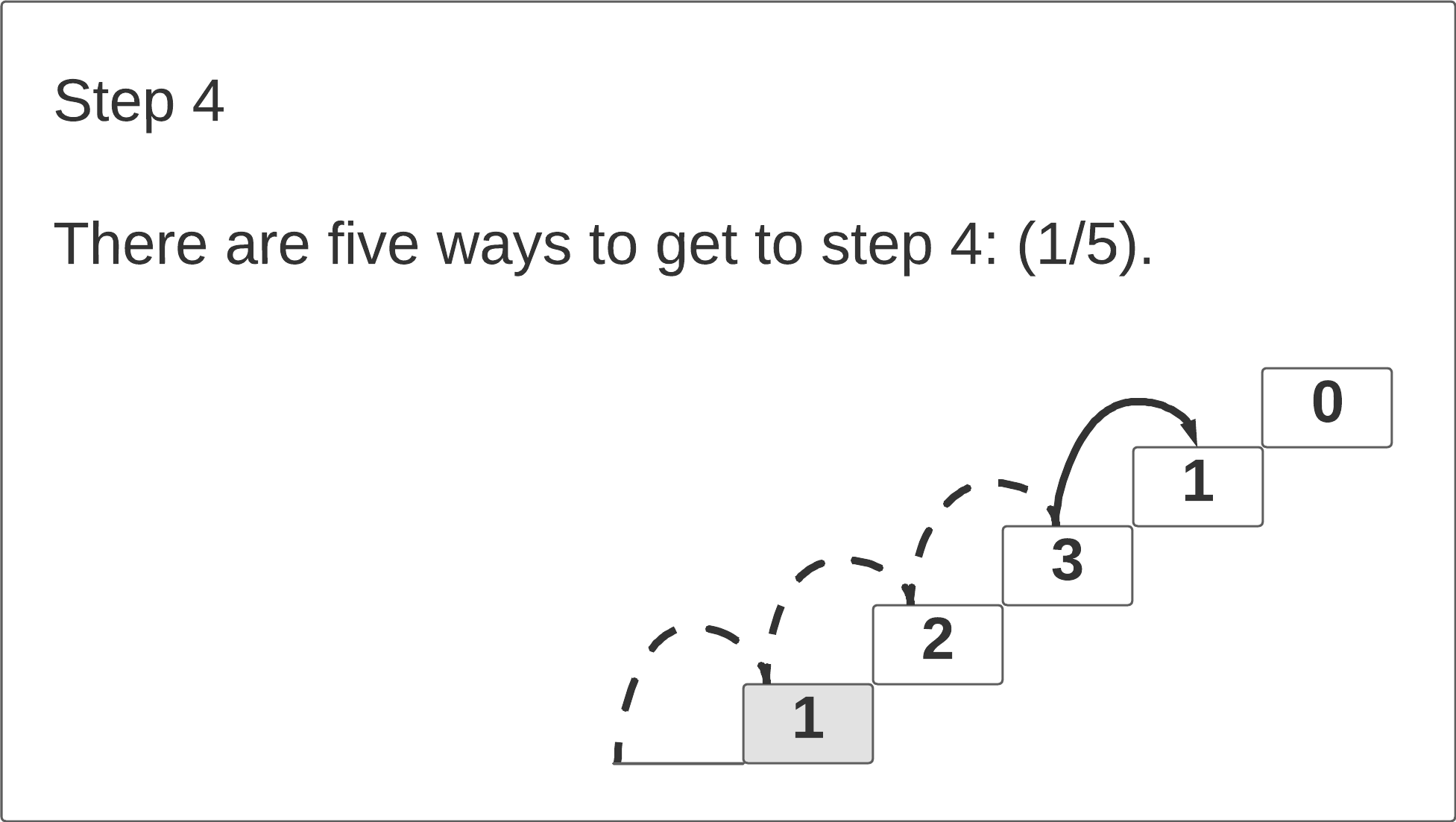
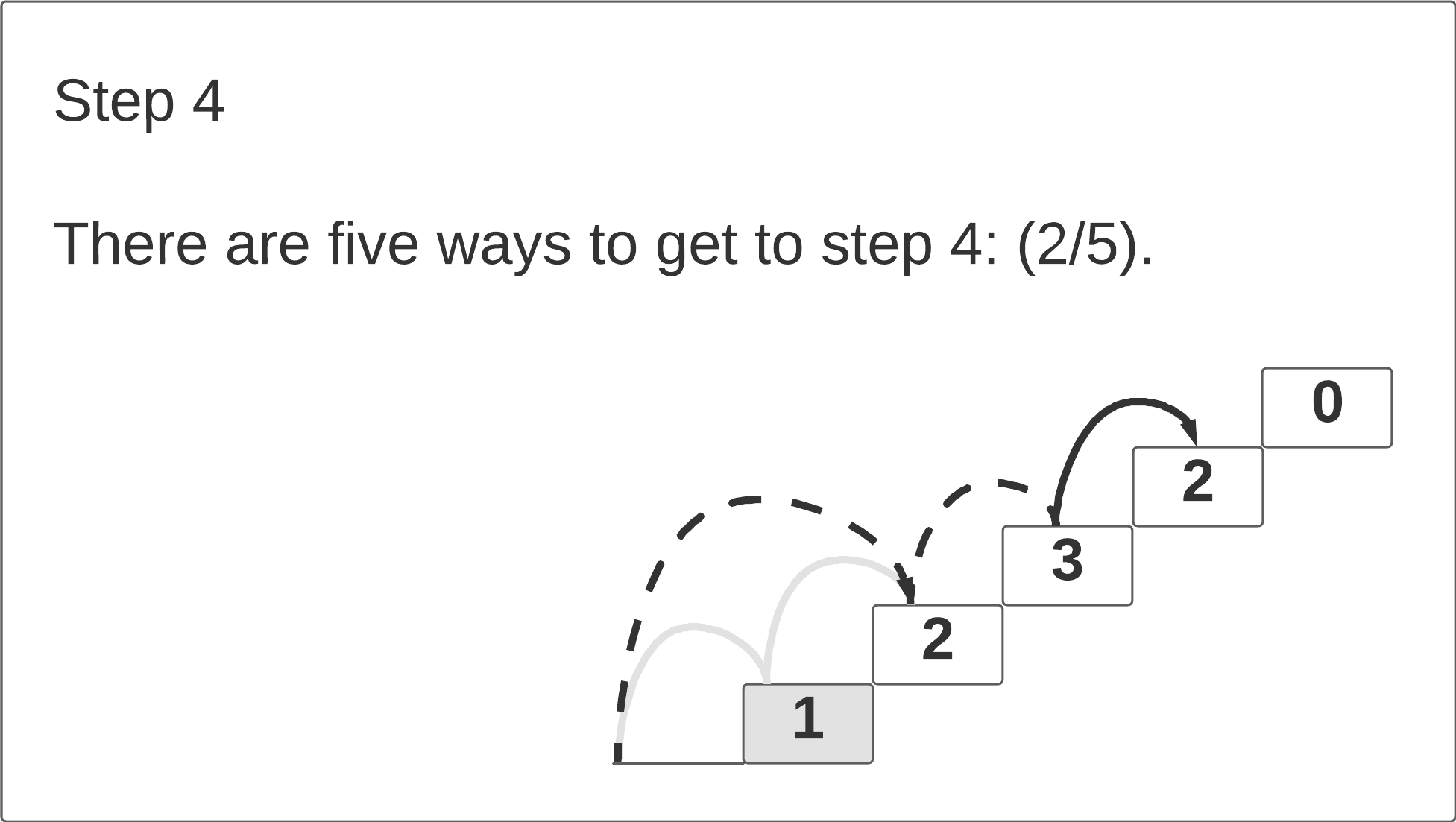
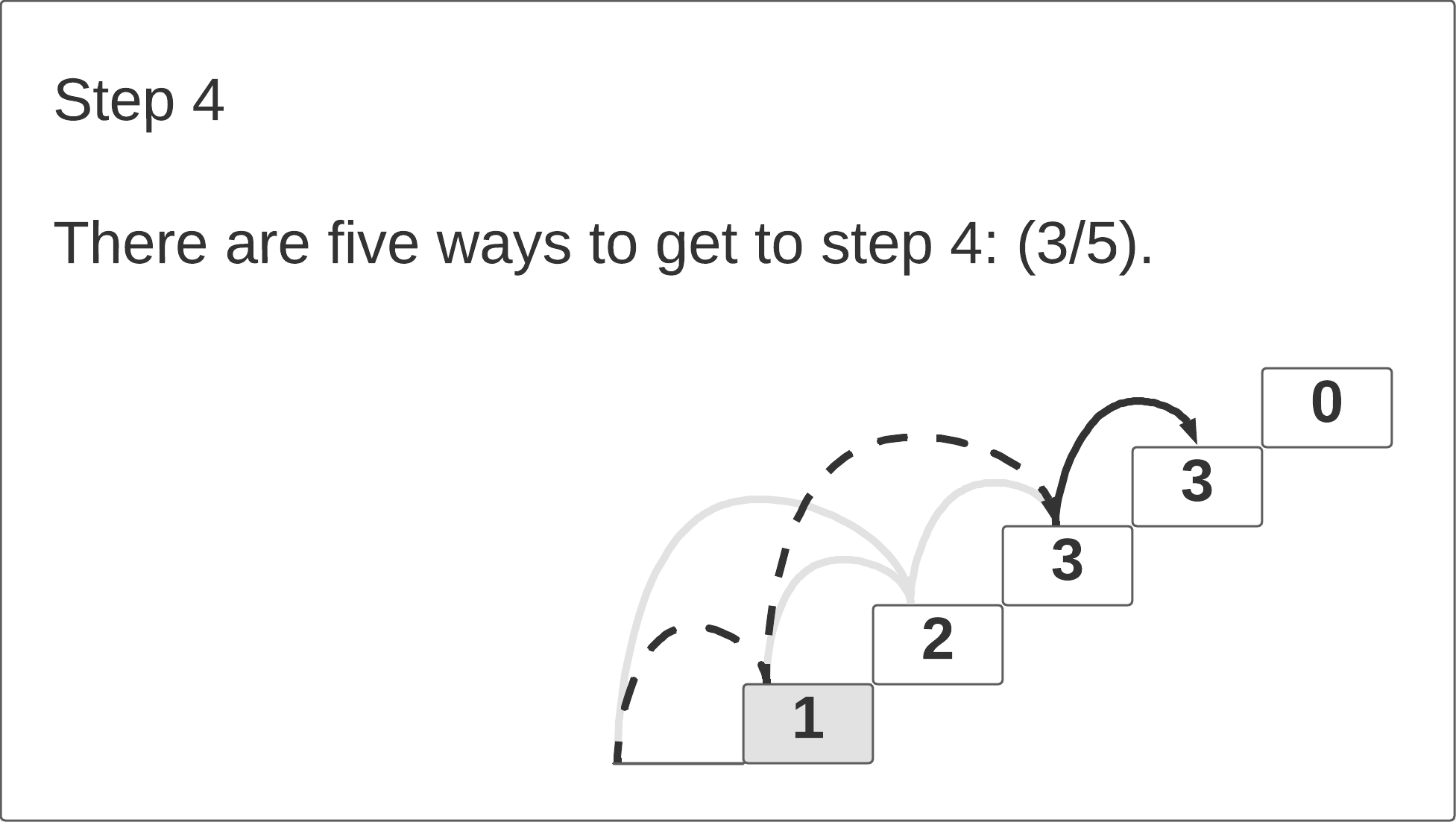
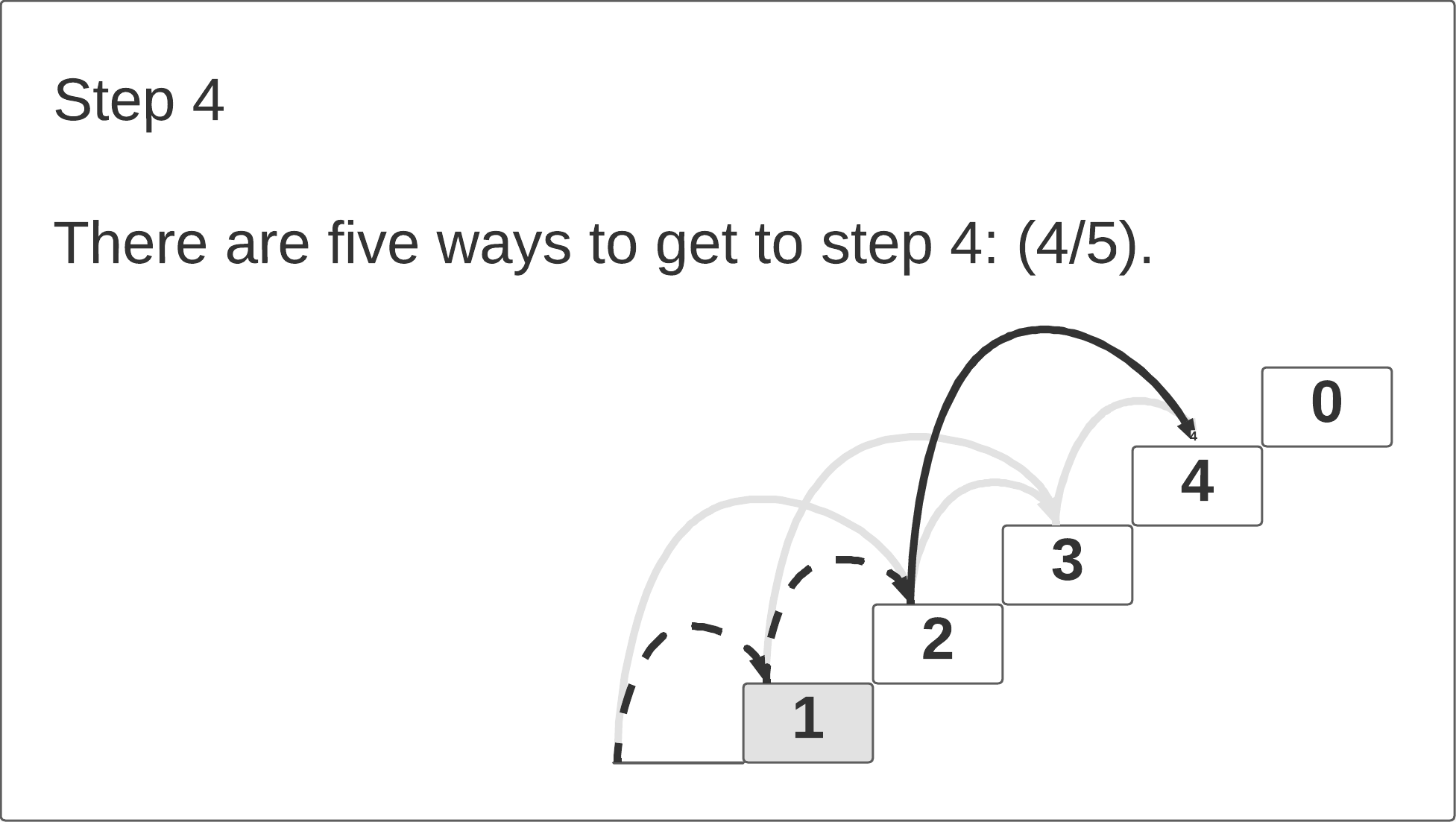
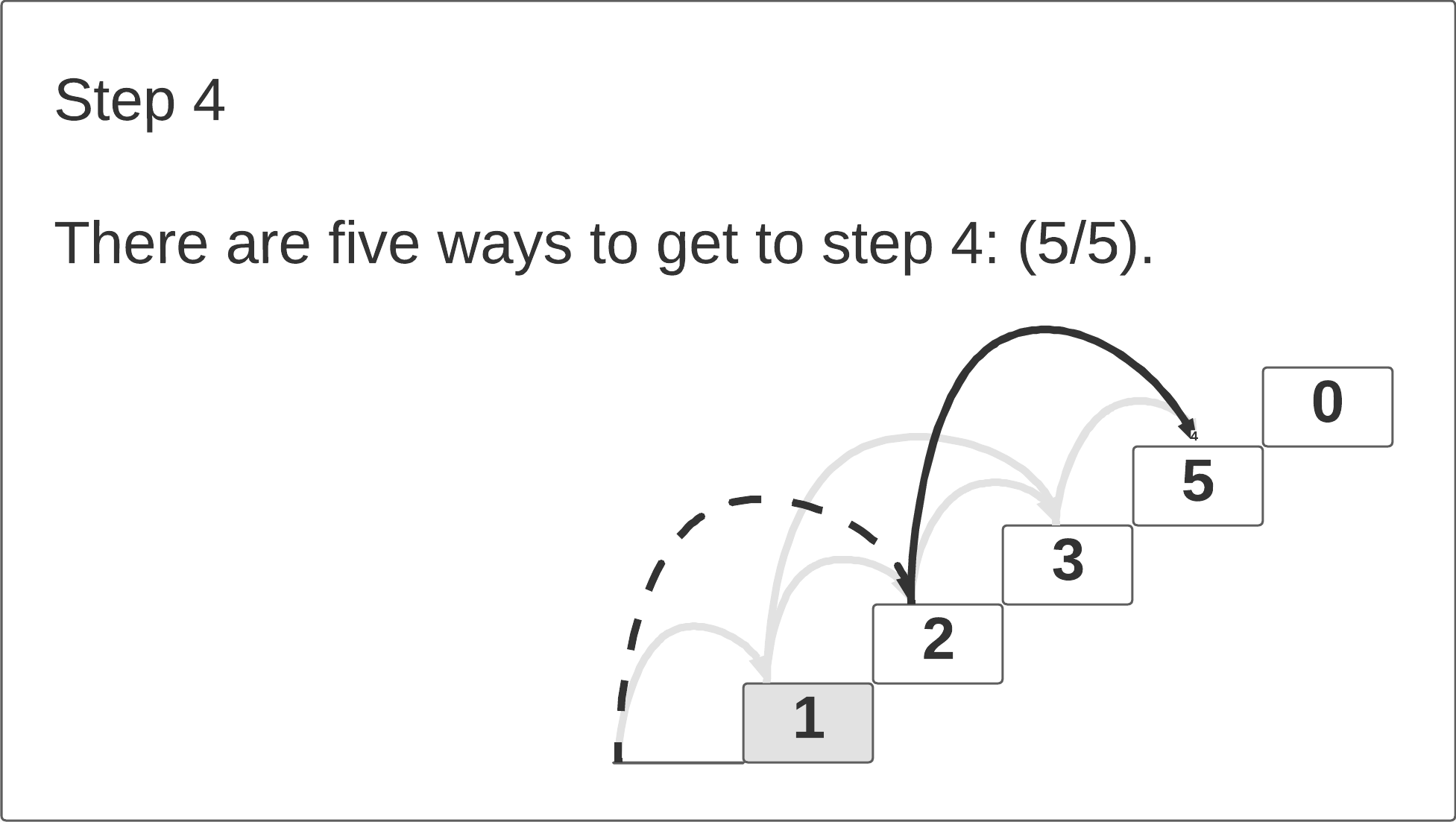
If we look at the first three steps, we notice that the number of path ways to reach each step Ni is equal to the sum of the pathways to the previous two steps N
i-1 + N
i-2. The click-through animation below illustrates this pattern.
If you recognized the Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... in this problem, you may be wondering what happened to the first 0, 1. How can we apply the Fibonacci sequence if we are only using a part of it? Many people question this point but gloss over it and just memorize the pattern. That’s great if you get this exact same question on an interview, but what if they change it up a bit?
This is actually a very common scenario. In science and engineering, mathematical models are typically valid over certain ranges of values. When you write solutions to Leetcode problems you need to think carefully about edge cases and you need to add conditions that guard against straying into territory where it no longer models the physics of the problem. Getting really comfortable with this concept will make interviews a lot easier.
When we walked through the possible pathways for the first three stairs, we ended up repeating work many time. When we counted all of the ways to reach stair 3, we ended up recounting all of the ways we could reach stairs 1 and 2. Since we are tracing out paths in this problem, we actually don’t need to retrace a path once we have it. Once work has been performed, we can cache the results and save computation time later on. This property is called overlapping subproblems.
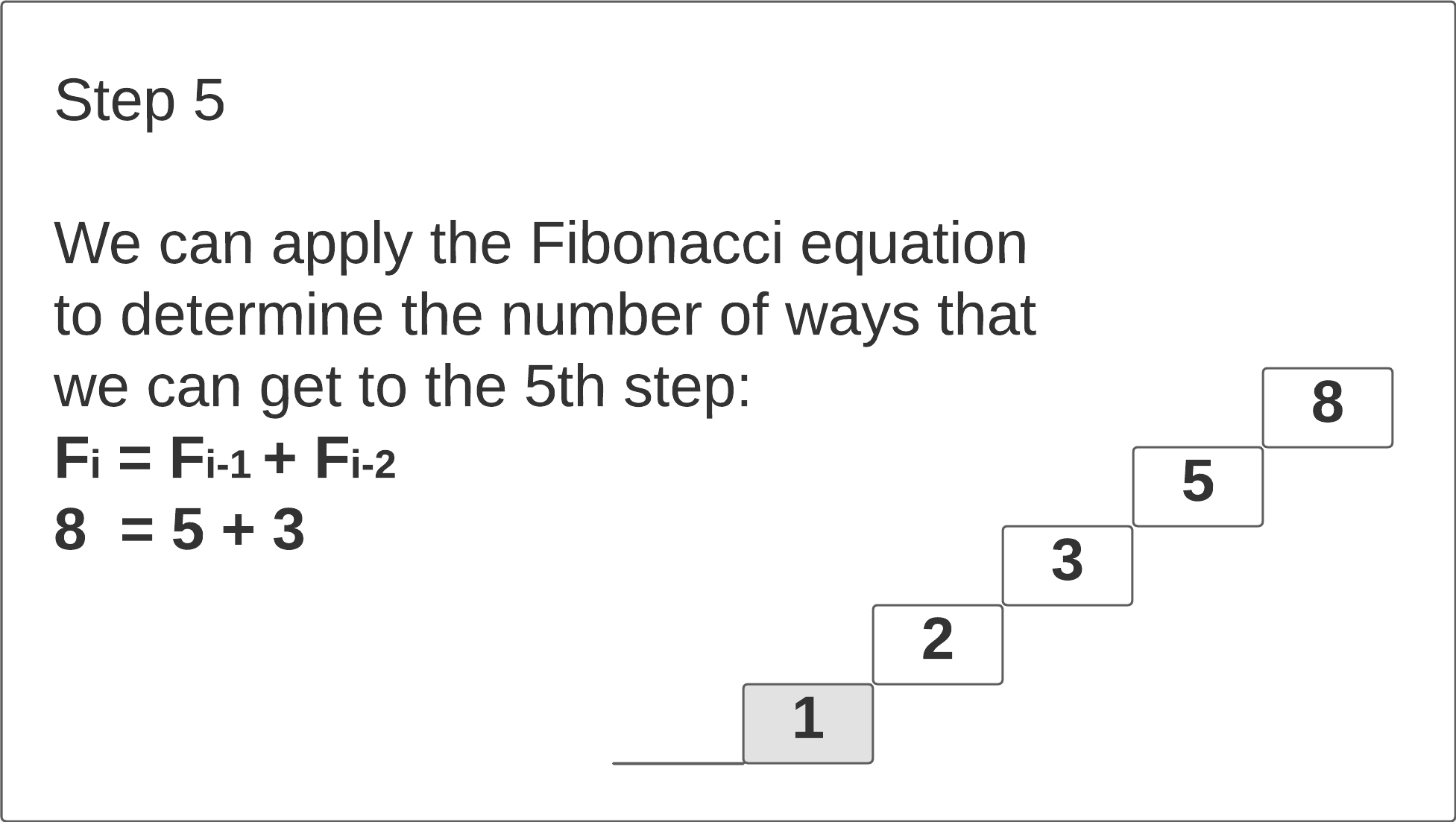
Since we know how many pathways there are to steps 4 and 3, we can easily determine how many pathways there are to step 5 by simply extending those pathways to it. Summing up the number of pathways to the previous two steps gives us the number of ways to reach the current step. In other words, we can construct the optimal solution to one problem by employing the optimal solution to subproblems. This property is called optimal substructure.
Based on these observations, we can conclude that this is a classic dynamic programming problem.
- overlapping subproblems
- optimal substructure
Python Solution
Top-down Dynamic Programming
class Solution:
def climbStairs(self, n: int, memo: dict = None) -> int:
"""
T: O(2^N)
S: O(N)
"""
# Initialize the memo hash map
if memo is None:
memo = dict()
# Since we know the answers to the 1-stair and 2-stair
# subproblems, we can use them as our base cases.
# Save the results of each subproblem > 2 in a hash map
# to eliminate duplicate work.
if n == 1:
return 1
elif n == 2:
return 2
elif n in memo:
return memo[n]
else:
memo[n] = self.climbStairs(n - 1, memo=memo) + \
self.climbStairs(n - 2, memo=memo)
return [n]
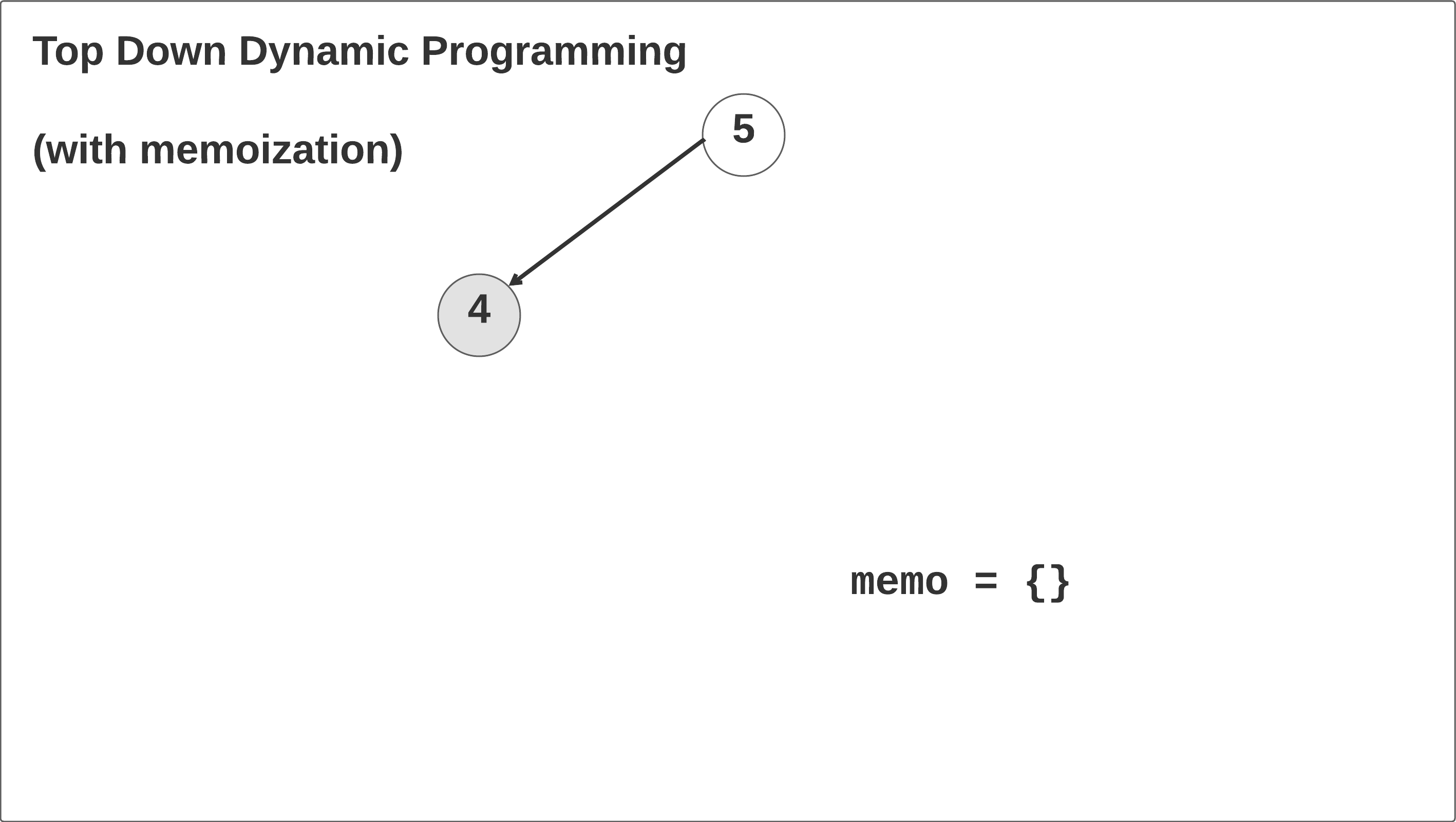
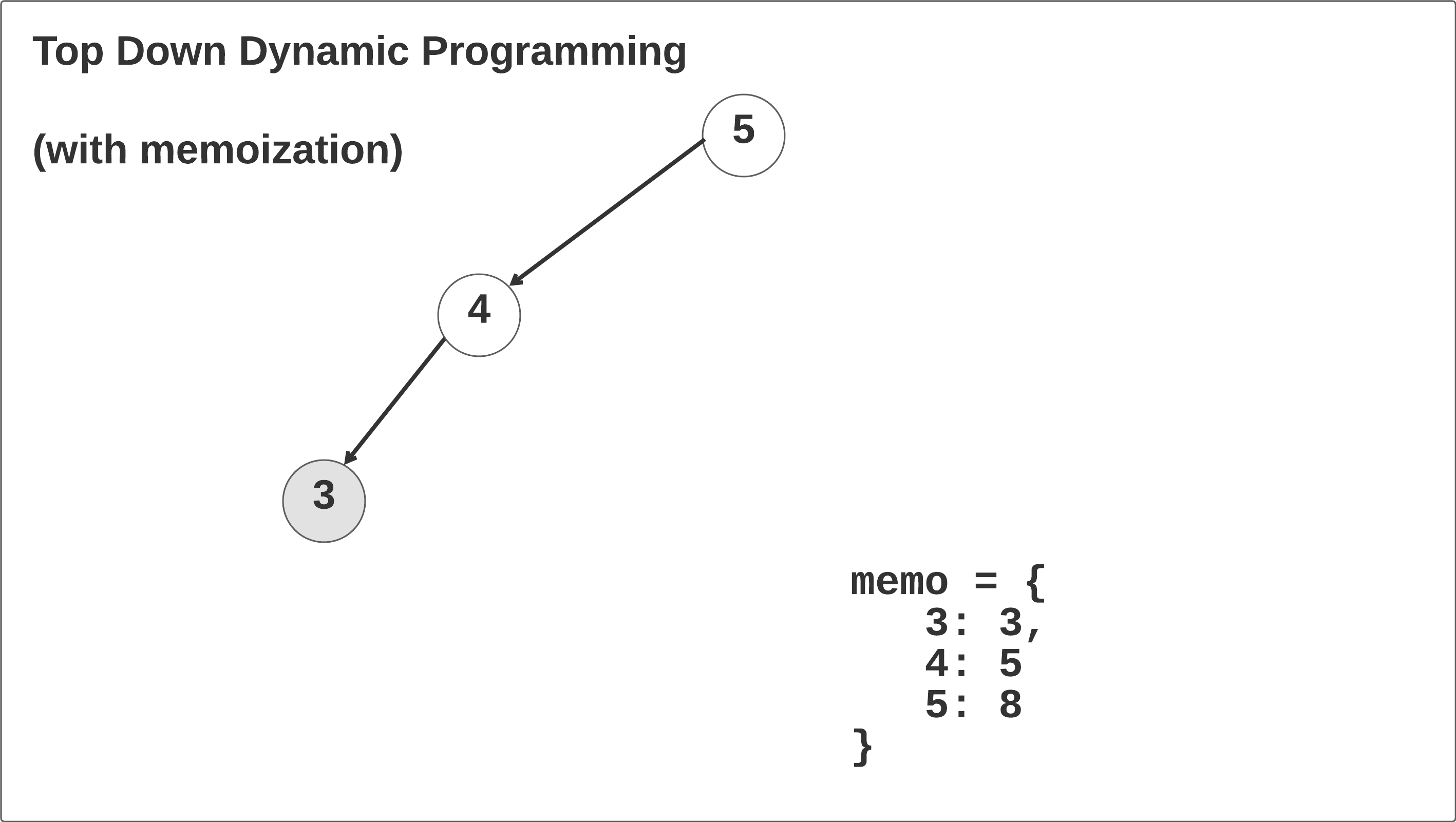
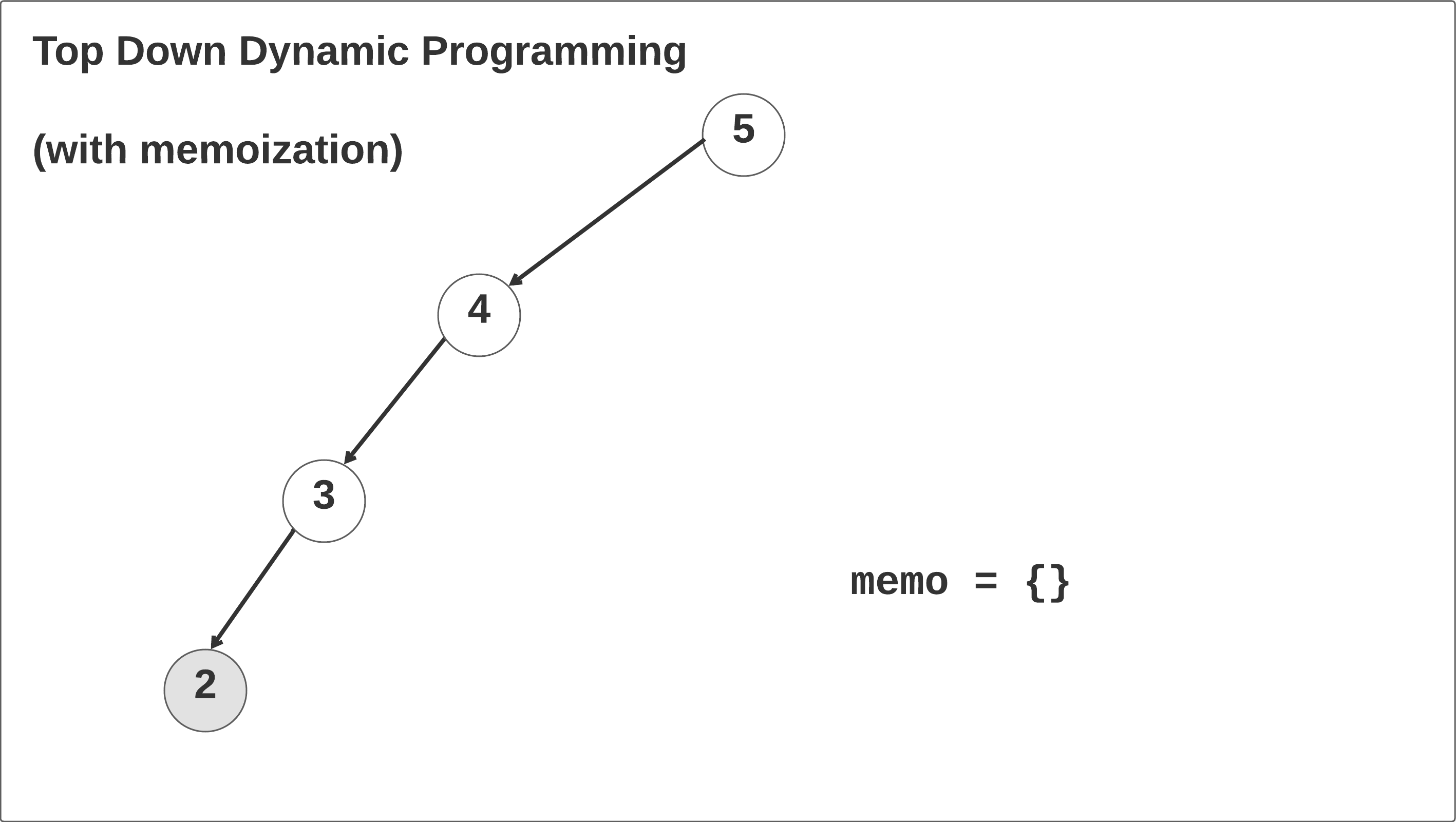
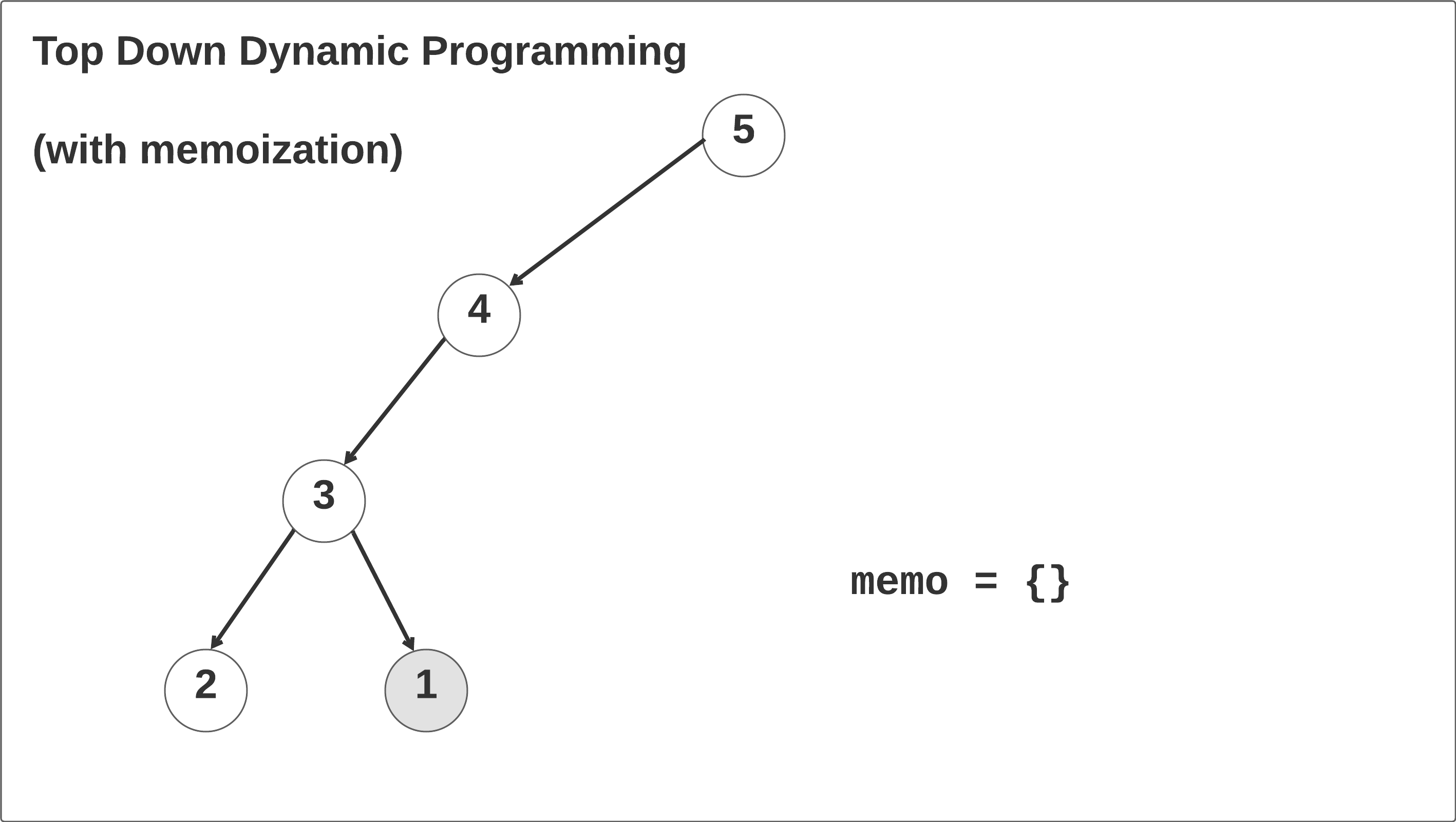
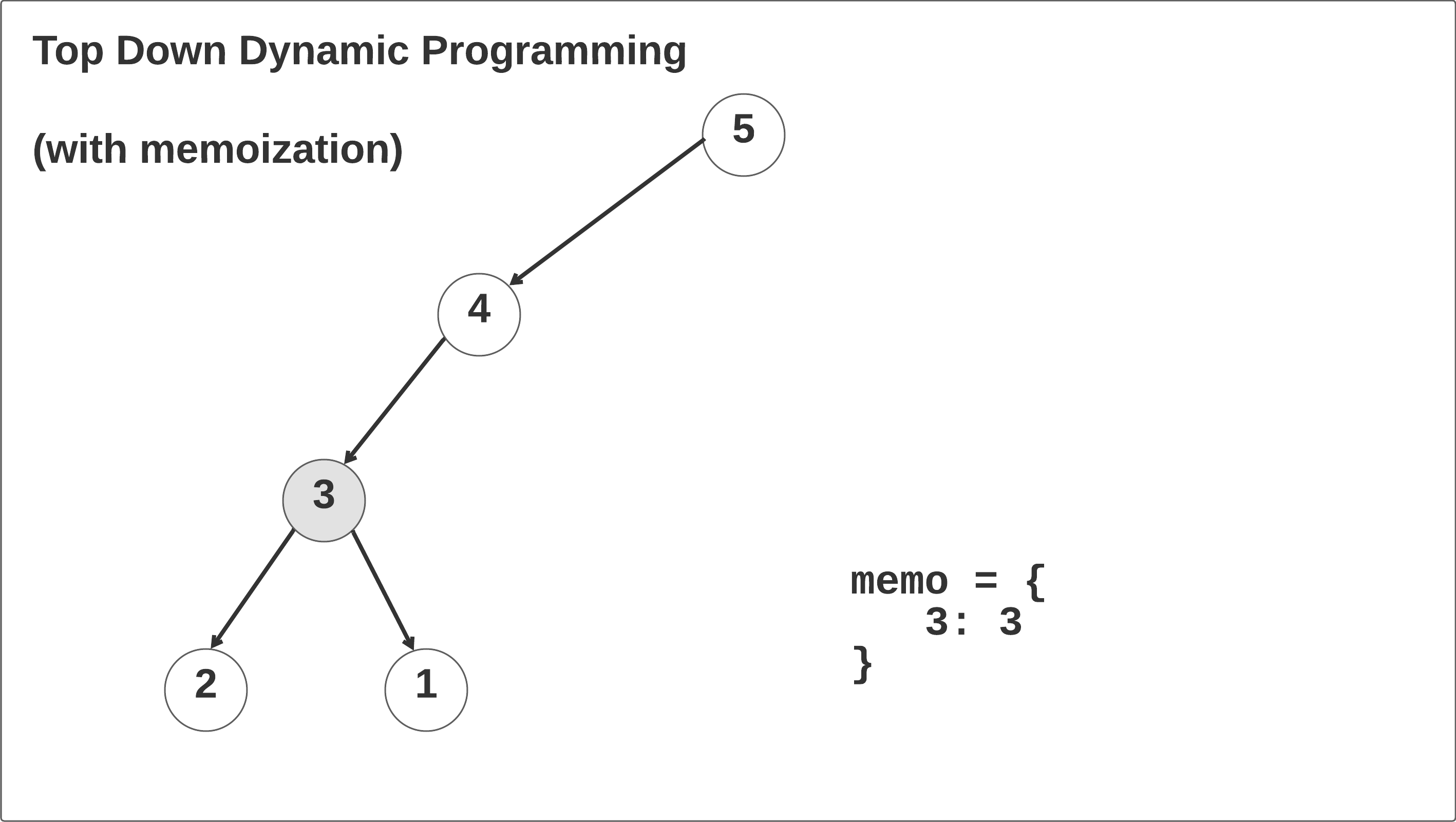
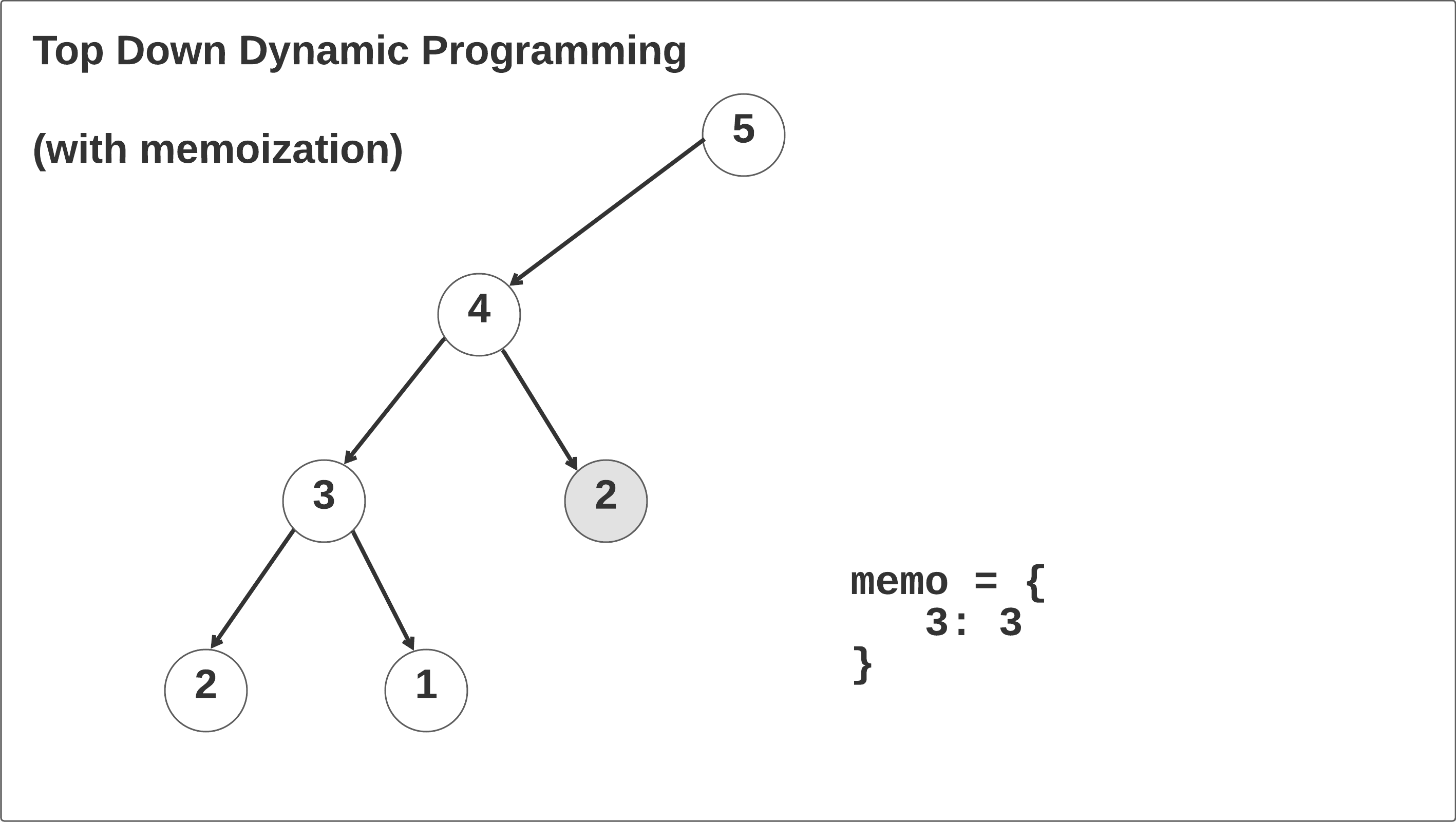
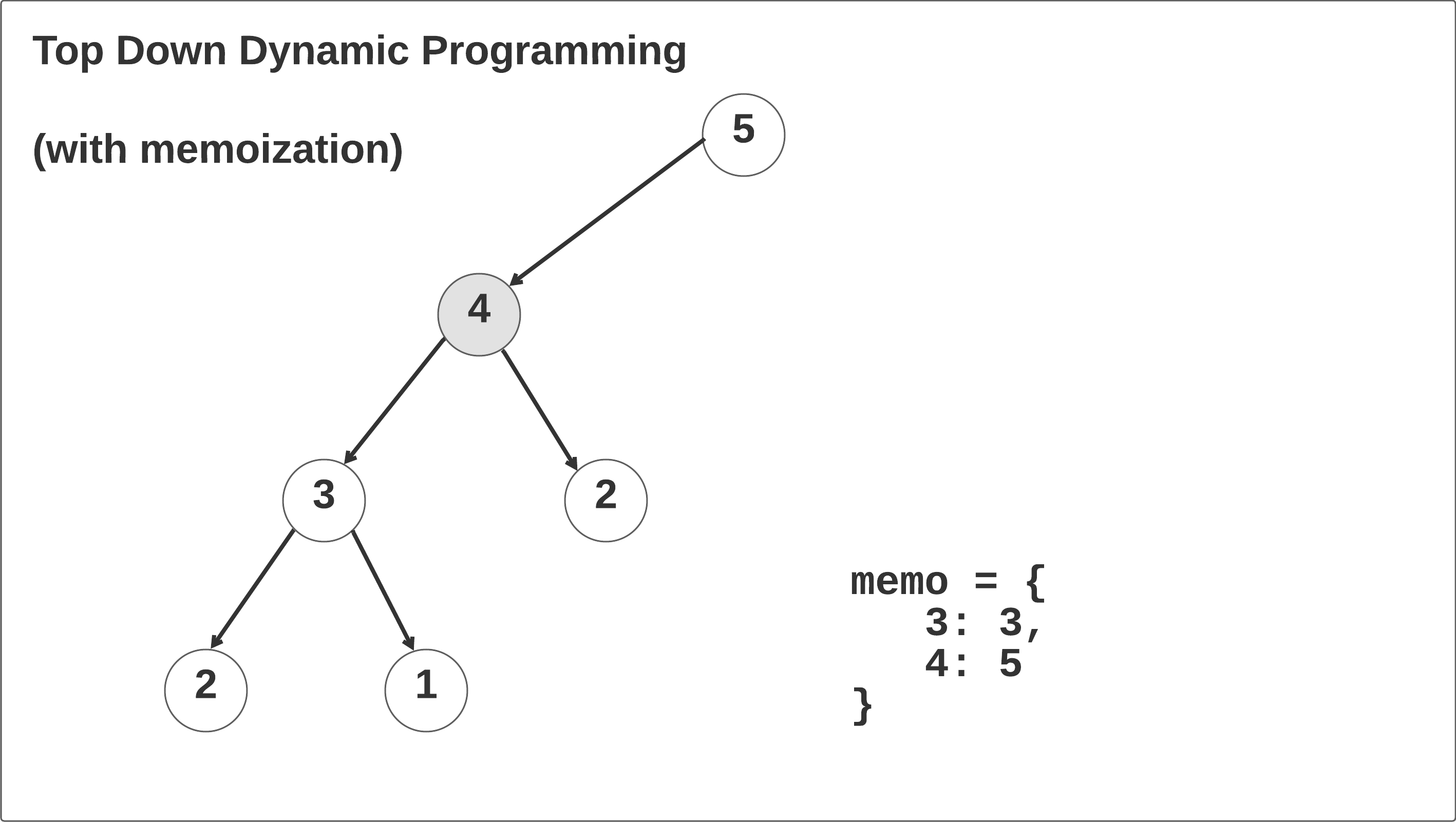
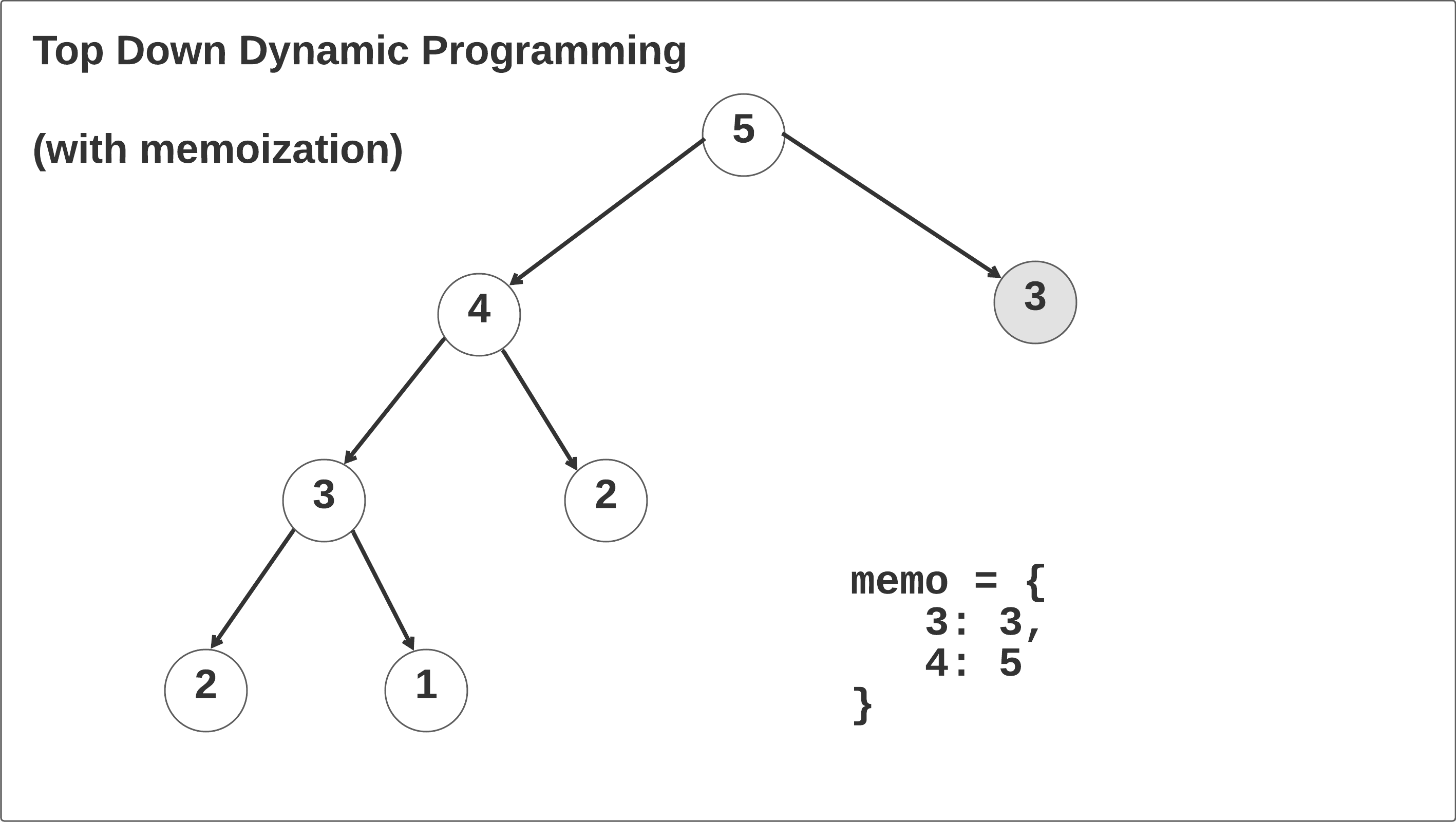
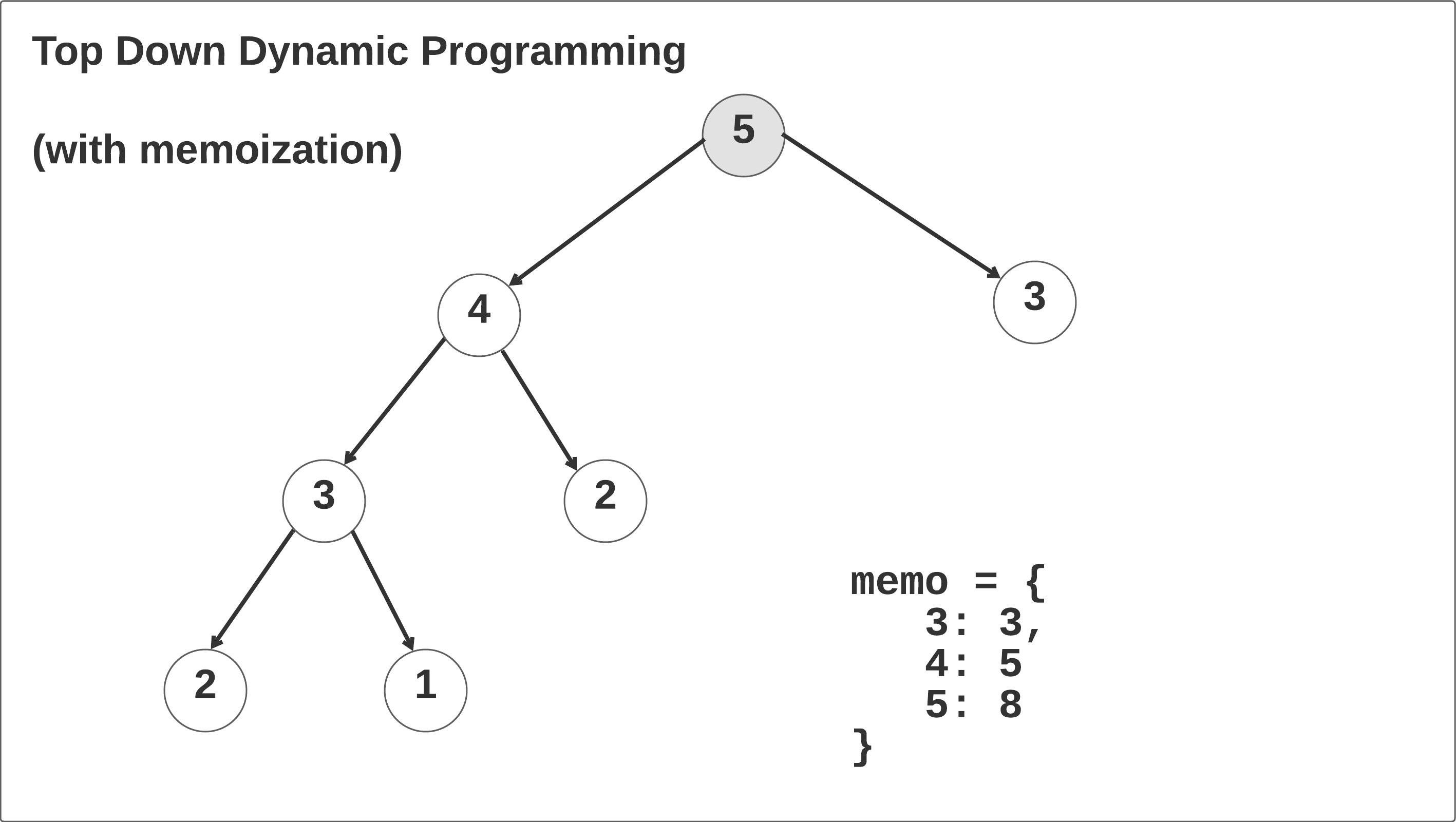
Let’s walk through the top-down dynamic programming solution with memoization and see what’s happening. Taking the time to thoroughly understand this example will help you understand recursion, memoization, and recurrence relations.
At the beginning, we initialize that memo hash map to a Python dictionary. Always set default parameters to None: see this stackoverflow question for more information. If you write memo: dict = {} in the constructor, the interviewer will think you are a Python noob.
In the first call, the memo hash map is initialized and the self.climbStairs(n-1, memo=memo) function is called recursively until the n == 2 base case is reached. When this case is reached in the left branch of the recursion tree, it returns 2 and then begins to recurse right: memo[3] = 2 + self.climbStairs(n - 2, memo=memo). We return the 1 base case up the call stack, save the result memo[3] = 2 + 1, and return memo[3] up one frame in the call stack. Click through the animation below to see this in action.
Bottom-up Dynamic Programming
If we translate the logic outlined in the Key Insights section above, we can easily write the following code.
class Solution:
def climbStairs(self, n: int) -> int:
"""
T: O(N)
S: O(N)
"""
# Since the recurrence relation need two previous values,
# it does not apply when n < 2. Account for this case and
# return 1.
if n == 1:
return 1
else:
# Since we know the answer to the 1-stair and 2-stair
# subproblems, we can iterate from the bottom up starting
# at index=2 and iterating up to index=n-1.
# As we increment our index variable, we calculate the
# answer for the step at the index and save the results in
# the dp array. Once we've iterated all the way to the top,
# the last element in the array is our answer.
dp = [0] * n
dp[0] = 1
dp[1] = 2
for i in range(2, n):
dp[i] = dp[i-1] + dp[i-2]
return dp[-1]